
The PSLE Math exam is renowned for its rigorous and sometimes perplexing questions that challenge even the best-prepared students. Being faced with such daunting tasks might seem overwhelming at first. However, the situation is far from hopeless. There are, in fact, proven strategies and approaches that can help students not only face these tough questions but answer them with confidence and clarity come exam day.
What are these “methods” that your child can leverage to ensure that they can approach the exam day and navigate the complexities of PSLE Math successfully? Consider these:
Understand the Challenge
Merely knowing that the PSLE Math exam will take place on 27 September 2024 is not enough to prepare effectively. Students must first familiarise themselves with the detailed exam format to navigate the challenges proficiently.
The PSLE Math exam comprises two written papers divided into three booklets, structured as follows:
| Paper | Booklet | Question Type | Total Marks | Duration |
|---|---|---|---|---|
| Paper 1 | Booklet A | 15 Multiple-Choice | 20 | 1 Hour |
| Booklet B | 15 Short-Answer | 25 | ||
| Paper 2 | 5 Short-Answer | 10 | 1 Hour 30 Minutes | |
| 12 Structured/Long-Answer | 45 |
Both papers are scheduled on the same day, with a break between them. But what is the objective behind implementing such a comprehensive exam for students?
The PSLE Math examination targets three core objectives:
- AO1 (Fundamental Knowledge): Memorise mathematical principles, rules, and formulas and execute basic calculations and algebraic processes.
- AO2 (Understanding and Application): Interpret data, grasp mathematical concepts, and apply these skills to different scenarios.
- AO3 (Advanced Thinking): Use logical reasoning to evaluate information, draw conclusions, and choose suitable methods to address complex problems.
Of the various goals listed by the Ministry of Education, students tend to find the advanced questions more intimidating than anything. This can adversely affect their performance if they do not develop the proper strategies to tackle them.
Pre-Exam Preparation
Success in the PSLE Math exam hinges not just on what students do during the exam but also on how well they prepare in the days and months leading up to it.
A fundamental part of this preparation involves mastering the basics. Ensuring that students have a robust understanding of essential mathematical concepts such as fractions, decimals, algebraic expressions, and geometry is crucial. These fundamentals form the building blocks upon which more complex problems are solved.
Additionally, regular practice with past PSLE Math papers is invaluable. This not only familiarises students with the format and typical questions they will face but also helps them develop and refine their problem-solving strategies. Working through these papers allows students to identify potential weaknesses in their knowledge and approach, providing a focused direction for further study. More importantly, this practice builds confidence, equipping students with the skills they need to tackle all the hard questions that tend to crop up during the examination.
Strategies for Tackling Hard PSLE Math Questions

Facing tough questions in the PSLE Math exam can feel daunting, but with the right strategies, you can turn those challenges into opportunities to showcase your problem-solving skills. Here’s how you can approach those tricky questions with confidence and clarity, ensuring you’re fully prepared to tackle whatever the exam throws your way.
1. Understanding the Question
Take the time to thoroughly read each question, encouraging students to absorb every detail. It is important to not just identify the main task of the question but also any specific conditions or constraints that could influence the approach. This step is crucial, particularly when questions are phrased in an unfamiliar way or include less common vocabulary. Students should focus on linking what is being asked to the Math concepts they’ve studied. This connection helps them utilise their knowledge flexibly, adapting to the question’s demands rather than falling back on rote memory.
While all this is being done, it’s also essential for students to remain composed, as a clear, calm mind is much better at parsing complex questions and thinking critically about the steps required to solve them.
2. Breaking Down the Problem
Teach your child the valuable skill of deconstructing a problem into smaller, more manageable segments. Encourage them to identify and highlight the key mathematical concepts or formulas relevant to the question. This approach simplifies the problem, making it less intimidating and more approachable. By understanding which parts of their mathematical toolkit to apply, students can systematically address each segment of the problem, enhancing their overall problem-solving strategy and increasing their confidence in handling complex questions.
3. Choosing an Approach
One effective method to approach complex PSLE Math questions is to utilise various problem-solving techniques, such as diagramming or logical reasoning.
Let’s consider a practical example to illustrate how to strategically tackle a challenging problem.
Example Question:
Maya has three identical containers of juice. She pours out 850 ml from each container. After pouring, the total amount of juice left in all three containers combined equals the amount of juice originally in one container. What was the original amount of juice in each container?
Common Misconception:
Some might quickly calculate 850 ml × 3, thinking this represents the original amount of juice in one container. However, this calculation actually represents the total amount of juice Maya poured out.
Strategic Approach A:
Here’s one way students can visually and logically solve this problem:
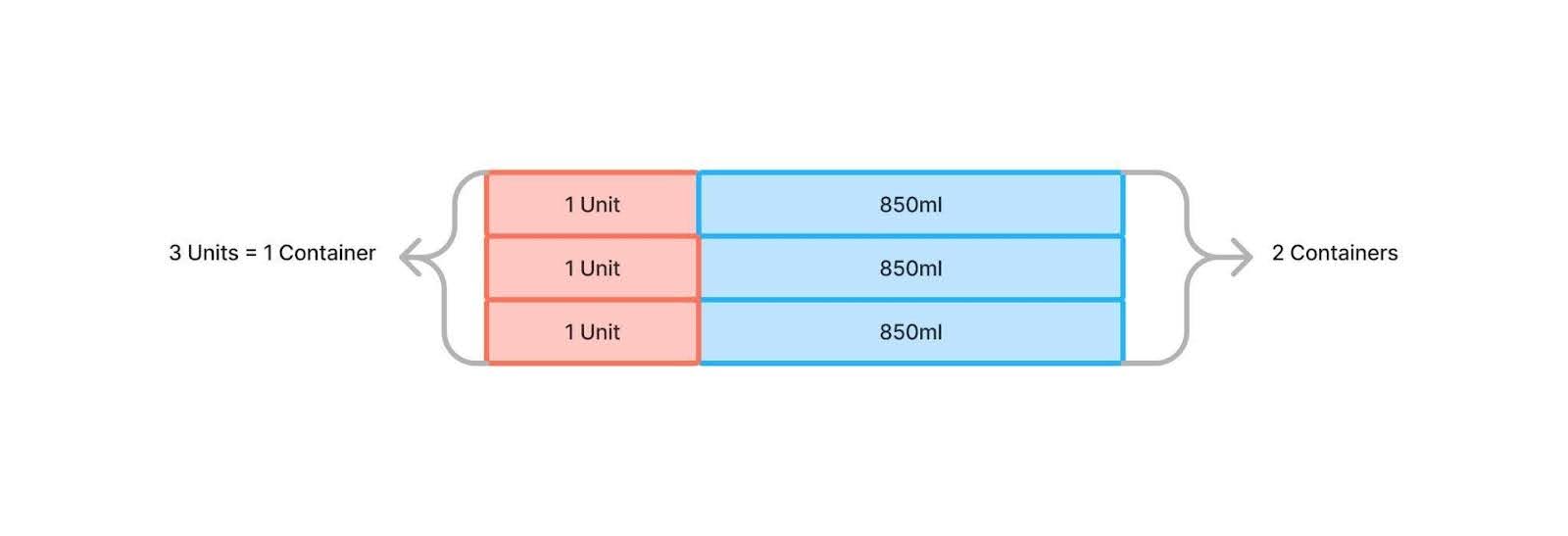
Step 1: Understand the Problem
- The problem tells us that the juice left in all three containers is equal to the juice that was originally in just one container. This means that the amount of juice Maya poured out (from all three containers) is the same as the amount of juice that was originally in two containers.
Step 2: Calculate the Total Amount of Juice Poured Out
- Maya pours out 850 ml from each of the three containers.
- Multiply the amount poured out from one container by 3:
- 850 ml × 3 = 2550 ml.
Step 3: Find the Original Amount in One Container
- Since the amount of juice poured out equals the amount of juice that was originally in two containers, divide the total amount by 2:
- 2550 ml ÷ 2 = 1275 ml.
- So, the original amount of juice in each container was 1275 ml.
Strategic Approach B:
Here’s another way to logically solve the same problem:
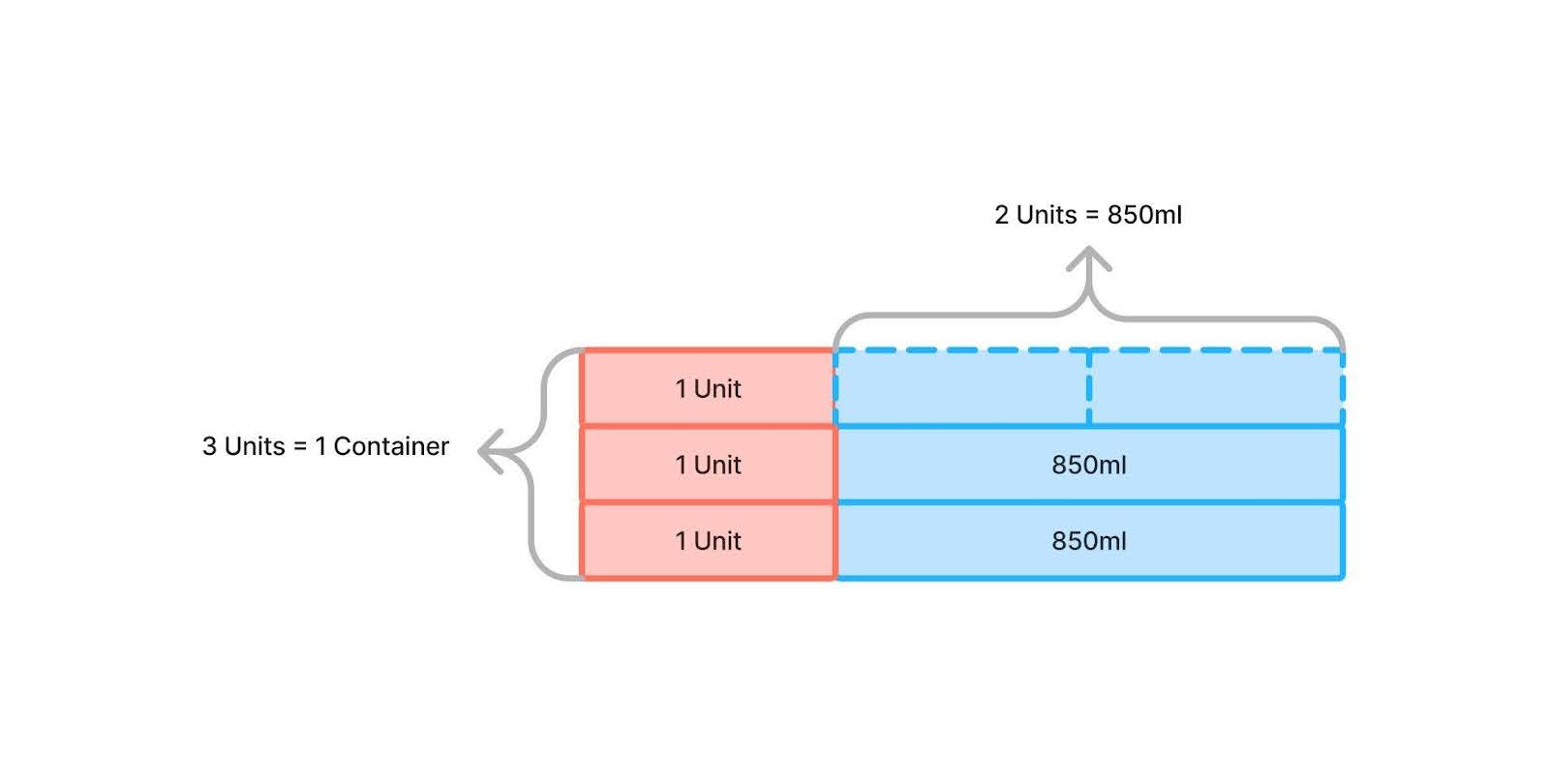
Step 1: Understand the Relationship Between the Containers and the Units of Juice
- The problem tells us that the amount of juice left in all three containers combined is equal to the amount of juice that was originally in just one container.
- Let’s think of the original amount of juice in each container as being made up of two parts: the juice that was poured out and the amount of juice that is left.
- Since the total amount of juice left in all three containers equals the original amount in one container, it means that what was left in each container after pouring is just one part (or one unit) of the original amount.
Step 2: Break Down the Units
- Imagine the original amount of juice in each container as 3 equal units: 1 unit for the juice left after pouring, and 2 units (which is 850 ml) that represent the juice that was poured out.
- This means that each container originally had 3 units of juice, and we know 850 ml is the amount of juice that makes up 2 units.
Step 3: Find the Original Amount
- If 850 ml represents 2 units, then to find the amount in one unit, divide 850 ml by 2:
- 850 ml ÷ 2 = 425 ml.
- Since 3 units make up the original amount of juice in one container, multiply the one unit amount by 3:
- 425 ml × 3 = 1275 ml.
- Therefore, the original amount of juice in each container was 1275 ml.
Using these methods helps clarify the problem setup and guides students through a logical sequence of steps, promoting a deeper understanding of how to manage complex problems systematically.
4. Problem-Solving Techniques
- Trial and Error: The path to mastering PSLE Math often involves navigating through complex problems that don’t always yield to the first solution attempt. Encourage students to embrace a trial-and-error approach. This process involves experimenting with various methods, which can be especially effective when traditional strategies don’t seem to fit. Systematic testing of different hypotheses or calculations not only builds resilience but also deepens understanding of mathematical concepts.
- Backtracking: In the journey through complex mathematical landscapes, backtracking is an essential skill. Teach your little ones that it’s okay to step back if they hit a roadblock. Encouraging them to review their calculations, reassess their assumptions, and double-check whether they have fully grasped the question can often illuminate missteps and reveal clearer paths to the solution. This method reinforces the importance of thoroughness and precision in math, ensuring students are confident in their final answers.
5. Managing Time Effectively
To maximise exam performance, it’s crucial for students to approach their PSLE Math paper strategically. Encourage them to first tackle the questions they find easiest or most familiar. This not only secures early marks but also boosts confidence as they progress to more challenging problems. Time management plays a pivotal role in this strategy.
Teaching students to recognise their strengths and start with those areas can make a significant difference in how they handle the pressure of the exam. It’s also important to practice setting time limits on different types of questions during their preparation. This helps them develop an intuitive understanding of how long to spend on each section, ensuring they have enough time to revisit and revise the tougher questions.
6. Review and Revision
It’s crucial to instil the habit of meticulous review in students preparing for the PSLE Math exam. Encourage them to always double-check their answers after completing each question. This involves revisiting calculations, ensuring that each step of the process is clear and correctly executed, and confirming that the final answer directly addresses the question. This practice not only helps catch common errors, such as simple arithmetic mistakes or misinterpretations of the question, but also reinforces the accuracy of their work. By making this a consistent part of their problem-solving routine, students can significantly reduce careless mistakes and boost their overall scores.
At TLS Tutorials, we specialise in Primary Math tuition, including P5 Math tuition, preparing students to excel in their PSLE Math exams when they head to P6. Our experienced tutors provide personalised guidance and proven strategies, helping students build a strong mathematical foundation and tackle even the toughest questions with confidence.
Join us to boost your child’s Math skills and turn exam challenges into opportunities for success.




