Common PSLE Math Questions: A Comprehensive Guide to Problem Sums
- 15 August 2025

PSLE Math challenges Primary 6 students to do more than recall formulas to find the right answer. They must interpret questions, apply logic, and solve complex problems, often within tight time limits. Some problem sums show up year after year in different forms, and yet they continue to trip up even the most prepared students. From fractions with remainders to tricky ratio transfers, these are the types of questions that often decide whether a student scores AL1 or falls a band short.
That’s why being familiar with the common PSLE Math questions and knowing how to solve them step-by-step is one of the smartest ways to revise. With the right approach, even complex problem sums become manageable, and confidence grows with every step that makes sense.
1. ‘Leftover’ Problems (Branching)
When a question describes a sequence of actions that leaves a remainder at the end, whether in money, time, or items, this is a clear signal to apply the Remainder Concept. This type of question shows up often in PSLE Math, especially within topics like fractions and percentages. What helps here is the “Branching” method, which is a visual approach that breaks a question into smaller, digestible parts.
Example: Ethan used 3/4 of his allowance on a game console. He then spent 2/3 of the remaining money on a gift. If he had $10 left, how much money did he have at first?
Step-by-step:
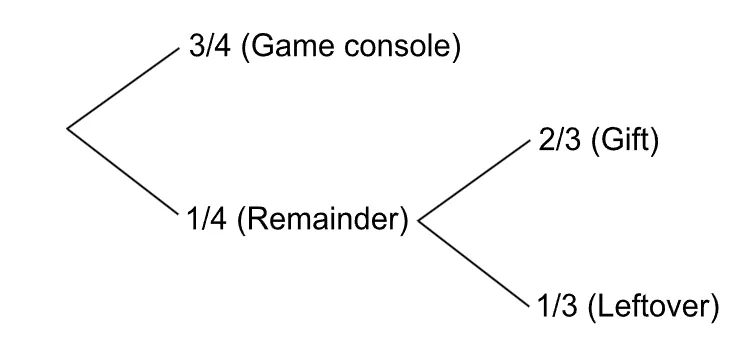
Fraction left after game console = 1 – 3/4 = 1/4
Fraction left after gift = 1/3 of 1/4 = 1/12
So $10 = 1/12 → Total = $10 × 12 = $120
This method works well for students who need to see how each fraction connects. It’s also an efficient way to reduce careless mistakes when handling layered operations.
2. The Equal Fractions Principle
Some PSLE problem sums ask students to compare two groups with different proportions, like how many students took the bus, or how many books were read. The trick in these questions? Set the fractions to equal numerators so that the comparison becomes simpler. This is where ratios and fractions meet.
Example: Out of all the children at a party, 3/4 of the boys and 5/6 of the girls wore hats. If the number of boys without hats was equal to the number of girls without hats, how many girls were there if there were 40 boys?
Step-by-step:
Boys without hats = 1 – 3/4 = 1/4
Girls without hats = 1 – 5/6 = 1/6
Since both groups have the same number of hatless children:
1/4 of 40 boys = 10 boys without hats
So, 1/6 of girls = 10 → Girls = 10 × 6 = 60 girls
3. Comparison Problems: More Than, Less Than, As Many As
When comparison terms like “more than,” “less than,” or “as many as” appear in problem sums, they’re typically inviting a model drawing approach. These questions challenge students to track changing quantities between two parties. The key is to represent the difference clearly using units, before and after, and adjust the models accordingly to show gains or losses.
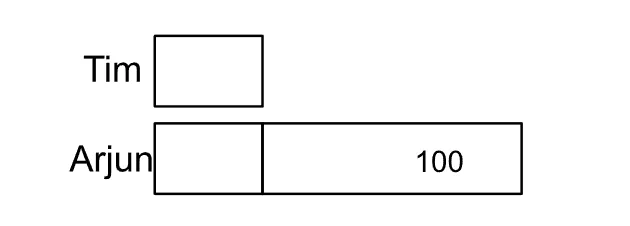
Example: Arjun had 100 more cards than Tim. After Arjun gave away 1/2 of his cards and Tim gave away 1/5 of his, Arjun ended up with 140 more cards than Tim. How many cards did Tim have at first?
Step-by-step:
Let Tim = 1 unit
Arjun = 1 unit + 100 (Arjun has 100 more)
Arjun gives away 1/2 → Arjun left = (1u + 100) ÷ 2
Tim gives away 1/5 → Tim left = 4/5
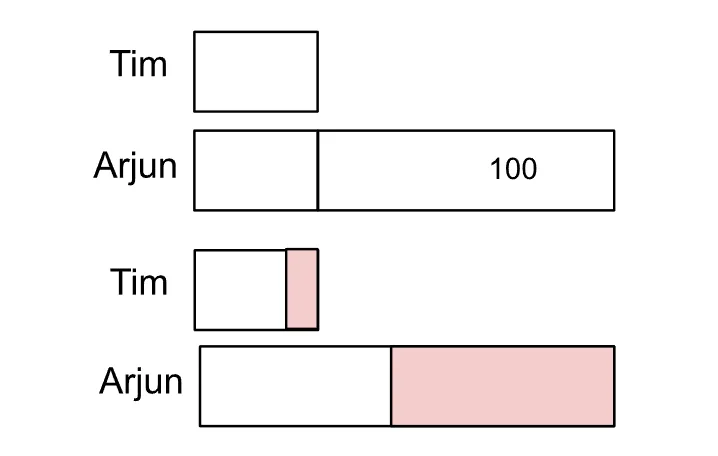
*Not drawn to scale
(1u + 100) ÷ 2 = 4/5 × 1u + 140
(1u + 100)/2 = 4u/5 + 140
Multiply everything by 10 to eliminate denominators:
5u + 500 = 8u + 1400
500 – 1400 = 8u – 5u
–900 = 3u
u = 300
Tim had 300 cards at first.
4. The Constant Total Concept
Some PSLE Math questions look like exchanges where one gives and one receives, but the total does not change. These are classic internal transfer problems where the key is to preserve the total and work with ratios before and after the exchange. Students need to spot when a problem involves a fixed quantity being moved, and then match that against changing ratios to find the unknowns.
Example: Liam and Noah had money in the ratio 7:5. After Liam gave $24 to Noah, they ended up with equal amounts. How much did Noah have in the end?
Step-by-step:
Set the initial total:
Liam : Noah = 7u : 5u → Total = 12u
Liam : Noah : Total
= 7 : 5 : 12
To become equal, both must end at 6u.
Liam : Noah : Total
= 6 : 6 : 12
Liam gave 1u (7u → 6u) → 1u = $24
Noah’s new total = 6u = 6 × $24 = $144
This technique encourages precise tracking and reinforces the idea that ratio problems often require thinking in units and seeing beyond the numbers alone.
5. The Everything Changed Concept (Units and Parts)
Some questions flip the script entirely, where both sides of the ratio change, and not in the same way. These “everything changed” problems tend to trip up students because you can’t rely on shortcuts. The Units and Parts method is one of the clearest ways to work through them.
Example: The ratio of Emma’s savings to Lily’s savings was 2:1. After Emma saved $60 and Lily spent $30, the new ratio became 4:1. How much money did Emma have at first?
Step-by-step:
Emma : Lily = 2u : 1u
Apply changes:
Emma → 2u + 60
Lily → 1u – 30
New ratio:
(2u + 60) : (1u – 30) = 4 : 1
Cross-multiply to eliminate the fractions:
1 × (2u + 60) = 4 × (1u – 30)
2u + 60 = 4u – 120
Solve for u:
4u – 2u = 60 + 120
2u = 180
u = 90
Find Emma’s initial savings:
2u = 2 × 90 = $180
6. The Grouping Concept
Grouping questions often pop up under shopping, seating, or packing scenarios and they’re all about logical bundling. The trick is to form one full “set” or “group” and then work backward or forward based on the total. Once the cost or value of one group is known, everything else falls into place.
Example: Arjun bought an equal number of notebooks and pens for $96. Each notebook costs $10 and each pen costs $6. How much did he spend on the notebooks?
Step-by-step:
Group 1 notebook and 1 pen:
10 + 6 = $16 per set
Find the number of sets:
96 ÷ 16 = 6 sets
Find the notebook cost:
6 × $10 = $60

7. The Number x Value Principle
When a question involves money or repeated values, the Number × Value principle becomes especially useful. This concept helps us determine the total value of a group by multiplying the quantity of each type of unit by its individual worth. Once the value of one group is known, we can work backwards to find how many such groups make up a total amount.
Example: A vending machine dispenses snacks in the ratio of 4 chips to 2 cookies. Each chip costs $1, and each cookie costs $2. If the total value of all snacks is $24, how many snacks are there altogether?
Step-by-step:
Ratio of chips : cookies
4 : 2
Find the value of 1 group:
4 chips × $1 = $4
2 cookies × $2 = $4
Total value per group = $8
Find the number of groups:
$24 ÷ $8 = 3 groups
Find the total number of snacks:
Each group = 4 + 2 = 6 snacks
3 groups × 6 = 18 snacks
8. Guess and Check / Assumption Method
The Assumption Method is an upgrade to traditional guess-and-check strategies. It speeds up problem solving by starting with a logical assumption, observing the resulting outcome, and adjusting based on a consistent pattern. This method is especially helpful when there’s a fixed total but differing unit values.
Example Question: There are 12 students. Each girl gets 4 sweets, each boy gets 2 sweets. The total number of sweets distributed is 32. How many boys are there?
Step-by-step:
Assume all 12 students are girls.
12 × 4 = 48 sweets
Replacing a girl with a boy reduces the total by (4 – 2) = 2 sweets
Required drop = 48 – 32 = 16 sweets
16 ÷ 2 = 8 boys
Final Answer:
8 boys and 4 girls
Check: (8 × 2) + (4 × 4) = 16 + 16 = 32 ✔️
Tackling difficult PSLE Math questions often comes down to recognising patterns and applying the right strategy. From remainder concepts to number-value principles and assumption methods, some of the most common Math questions that stump Primary 6 students require more than rote memorisation. They demand structured thinking, logical steps, and plenty of practice.
If your child is struggling with these Primary School Math questions, it’s time to seek support. At TLS Tutorials, we specialise in guiding students through PSLE Math questions with not just solutions, but clarity. Our Primary 6 Math tuition programme breaks down even the trickiest PSLE questions with answers in a way that builds confidence and deep understanding.
Looking for a proven Primary Math tuition centre in Singapore? Join us today and watch your child tackle their next challenge with certainty.
